In the realm of linear algebra, eigenvectors hold a significant position. They are indispensable in various fields including mathematics, physics, engineering, and computer science. In this article, we delve into the concept of eigenvectors, their importance, and how they can be calculated using an eigenvector calculator.
What are Eigenvectors?
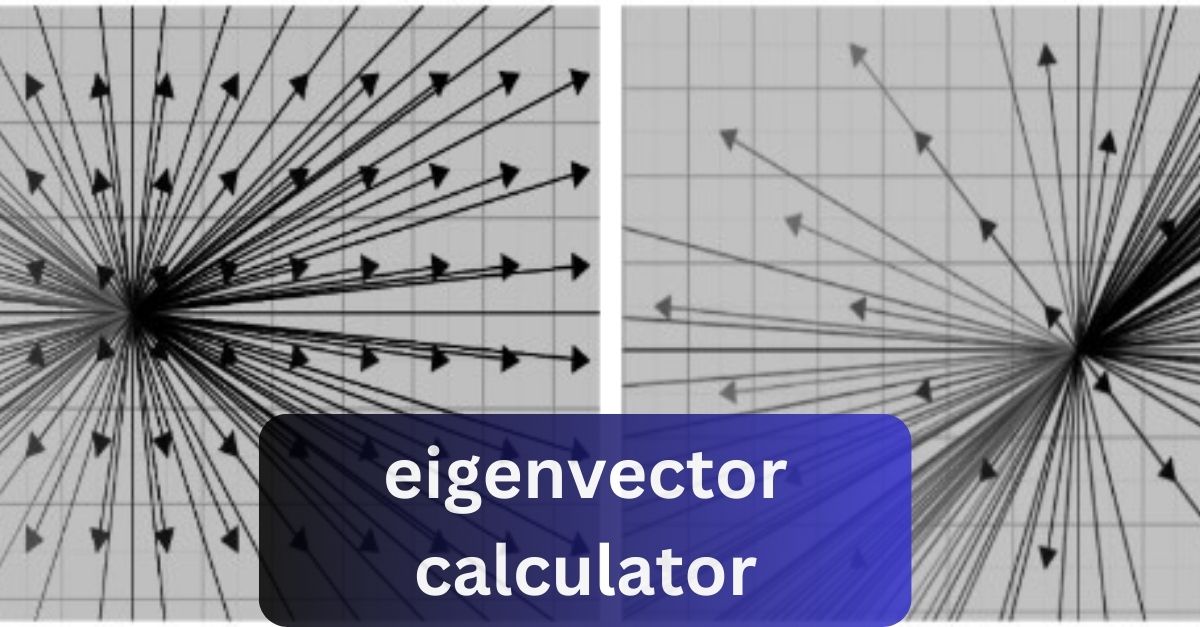
Eigenvectors are vectors that maintain their direction under a linear transformation, albeit they may be stretched or shrunk. In simpler terms, when a matrix operates on an eigenvector, the resulting vector is parallel to the original vector. This unique property makes eigenvectors crucial in understanding the behavior of linear transformations.
Read industrial swag nguyen duy tri • acid madness • 2023
Significance of Eigenvectors:
Eigenvectors find applications in a plethora of fields. In quantum mechanics, they represent the possible states of a quantum system. In structural engineering, they aid in analyzing the stability of structures under various loads. Moreover, in image processing, eigenvectors are utilized in facial recognition algorithms. Understanding eigenvectors is thus essential for tackling complex problems across disciplines.
Eigenvalues and Eigenvectors:

Eigenvalues are scalar values associated with eigenvectors, representing the factor by which the eigenvector is scaled during the transformation. Together, eigenvalues and eigenvectors provide insights into the characteristics of linear transformations. While eigenvalues quantify the scaling factor, eigenvectors depict the direction unaffected by the transformation.
Calculating Eigenvectors:
The process of computing eigenvectors involves solving a system of linear equations. Given a square matrix
�
A and an eigenvector
�
v, the equation
��=��
Av=λv must hold, where
�
λ is the corresponding eigenvalue. By rearranging terms, we obtain
(�−��)�=0
(A−λI)v=0, where
�
I is the identity matrix. Solving this equation yields the eigenvectors and their corresponding eigenvalues.
Eigenvector Calculator: A Handy Tool
For complex matrices or large datasets, manual computation of eigenvectors can be cumbersome and prone to errors. To alleviate this challenge, eigenvector calculators provide a convenient solution. These online tools efficiently compute eigenvectors and eigenvalues for a given matrix, saving time and effort.
Using an Eigenvector Calculator:
To use an eigenvector calculator, input the matrix for which you want to find eigenvectors. The calculator then employs computational algorithms, such as the QR algorithm or the power iteration method, to compute the eigenvectors and eigenvalues. Once the computation is complete, the results are displayed, enabling users to analyze the eigenvectors and their corresponding eigenvalues.
Read nguoi ra di nguyen si kha • rainy day memories • 2023
Properties of Eigenvectors:
Eigenvectors possess several intrinsic properties that make them valuable tools in linear algebra. These properties include orthogonality, linear independence, and stability under linear transformations. Understanding these properties enhances the comprehension and utilization of eigenvectors in various applications.
Applications of Eigenvectors:
Eigenvectors find extensive applications in diverse fields ranging from physics and engineering to data analysis and machine learning. Explore how eigenvectors are employed in quantum mechanics, structural analysis, signal processing, and dimensionality reduction techniques like Principal Component Analysis (PCA). Understanding these applications showcases the versatility and significance of eigenvectors in real-world scenarios.
Eigenvalues vs. Eigenvectors: A Comparative Analysis
While eigenvalues and eigenvectors are closely related concepts, they serve distinct purposes in linear algebra. Delve into the differences between eigenvalues and eigenvectors, their roles in matrix transformations, and how they are computed. Understanding the nuances between eigenvalues and eigenvectors elucidates their complementary nature in analyzing linear systems.
Advanced Techniques for Eigenvector Computation:
In addition to traditional methods like the power iteration method and QR algorithm, advanced techniques have been developed for efficiently computing eigenvectors of large matrices. Explore iterative methods, such as the Arnoldi iteration and Lanczos algorithm, as well as parallel and distributed computing approaches. Understanding these advanced techniques expands the computational toolkit for tackling eigenvector computation challenges in modern applications.
Read not commission nguyen duy tri • acid madness • 2023
Eigenvector Decomposition: Unveiling Matrix Structure
Eigenvector decomposition, also known as spectral decomposition or eigendecomposition, is a powerful technique in linear algebra used to decompose a square matrix into its constituent eigenvectors and eigenvalues. This decomposition provides valuable insights into the structural properties of the matrix, revealing its fundamental characteristics and facilitating various analyses.
By expressing the matrix as a linear combination of its eigenvectors weighted by their corresponding eigenvalues, eigenvector decomposition simplifies tasks such as matrix diagonalization, matrix exponentiation, and solving systems of differential equations.
Moreover, eigenvector decomposition plays a crucial role in spectral graph theory, where it aids in analyzing the connectivity and clustering patterns of networks represented by adjacency matrices.
Eigenvectors in Machine Learning: Dimensionality Reduction and Feature Extraction
In the realm of machine learning, eigenvectors serve as indispensable tools for dimensionality reduction and feature extraction. Techniques like Principal Component Analysis (PCA) leverage eigenvectors to transform high-dimensional data into a lower-dimensional subspace while preserving the variance in the data.
By identifying the principal axes of variation, PCA enables efficient data compression, visualization, and noise reduction, thereby facilitating tasks like classification and clustering. Additionally, eigenvectors play a crucial role in other dimensionality reduction methods such as Singular Value Decomposition (SVD) and Linear Discriminant Analysis (LDA).
Through feature extraction, eigenvectors enable the extraction of informative features from raw data, enhancing the performance and interpretability of machine learning models. Understanding the role of eigenvectors in machine learning empowers practitioners to leverage dimensionality reduction techniques effectively and extract meaningful insights from complex datasets.
Eigenvectors in Quantum Mechanics: Understanding Particle States
In quantum mechanics, eigenvectors play a central role in representing the states of quantum systems and predicting their behavior. In the context of the Schrödinger equation, the wavefunction of a quantum system represents its state vector, which can be decomposed into eigenvectors of the Hamiltonian operator.
These eigenvectors, known as stationary states or energy eigenstates, correspond to the possible energy levels of the system, while the corresponding eigenvalues represent the energies associated with each state. By observing how these eigenvectors evolve over time, quantum physicists can predict the probabilities of different outcomes and understand the dynamics of quantum systems.
Eigenvectors also play a crucial role in quantum algorithms, where they are utilized in tasks such as quantum state preparation, quantum simulation, and quantum error correction. Understanding the role of eigenvectors in quantum mechanics is essential for grasping the fundamental principles of quantum theory and advancing research in quantum computing and quantum information science.
Conclusion:
Eigenvectors play a pivotal role in diverse fields, offering valuable insights into linear transformations. Understanding eigenvectors and their corresponding eigenvalues is fundamental for solving complex problems across various disciplines. With the aid of eigenvector calculators, the process of computing eigenvectors becomes more efficient, allowing researchers and practitioners to focus on interpreting results rather than tedious computations.
Read Also: